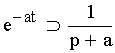Question de cours: (1,5 pt)

Sachant que 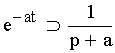, donner l’image par la transformation de Laplace de cos( wt).

Exercice n°1: (7 pts)

1) Résoudre .(5 pts)

2) Calculer y si y(0) = 5, et y’(0) = .(2 pts)

Exercice n°2: (11,5 pts)

Soit la matrice [A]= .

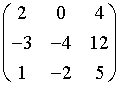Partie 1: (6,5 pts)

a) Déterminer l’équation caractéristique notée D( l).(0,5 pt)

b) Déterminer les valeurs propres de la matrice qu’on notera

l₁, l ₂, l₃ dans l’ordre croissant.(1,5 pt)

c) Vérifier que 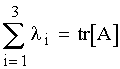.(0,5 pt)

d) Déterminer les vecteurs propres associés.(3 pts)

e) Donner l’expression de la matrice [D] et de la matrice de passage

[P] de l’ancienne base à la nouvelle base .(1 pt)

Partie 2: (5 pts)

a) Calculer dét[P].(0.5 pt)

b) Calculer [P]^-1.(1,5 pt)

c) Sans exprimer , ni , démontrer par récurrence que
( ) où [D] est la matrice diagonale semblable à A dans la nouvelle base de vecteurs propres .(1 pt)

d) Calculer [D]ⁿ ( ).(1 pt)

e) Calculer [A]ⁿ ().(1 pt)