Les exercices sont indépendants et peuvent être traités dans l'ordre de votre choix.

Il sera tenu compte de la rédaction

Exercice n°1: Limites. ( 3 pts)

Calculer la limite suivante: .

Exercice n°2: Optimisation. ( 8 pts)

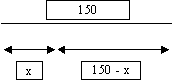
En coupant un fil de fer de 1,5 m en deux morceaux, on souhaite former une circonférence et un triangle équilatéral.

1) A quel endroit x faut-il couper le fil pour que l'aire formée par ces deux surfaces soit minimale (x pour le périmètre de la circonférence et 150 - x pour celui du triangle) ?

2) A quel endroit x faut-il couper le fil pour que l'aire formée par ces deux surfaces soit maximale ?

On rappelle que

Pcirconférence = 2p.R	Acirconférence = p.R2	R: rayon
Ptriangle équilatéral = 3a	Atriangle équilatéral =	a: côté

Exercice n°3: Nombres complexes. ( 9 pts)

m étant un paramètre réel, on considère le nombre complexe:

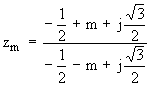avec

a) Calculer la partie réelle et la partie imaginaire de z_m .

b) Déterminer la valeur de m pour lesquelles la partie réelle de z_m est nulle. Présenter z_m sous forme exponentielle pour chacune des valeurs de m obtenue.

c) Résoudre dans l'ensemble des complexes l'équation ( désigne la valeur de z_m pour m = -1).

d) Calculer .
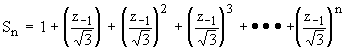