Exercice n°1:( 2 points)

A l'aide de l'annexe jointe intégrer I = .

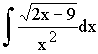Exercice n°2: (3 points)

Soit y = Arctan(x) + Arctan(1/x).

En passant par la dérivée, calculer y.

Partie A: ( 9 points)

Soit la fonction 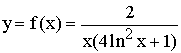. (on précise ln²x = (lnx)²)

1°) Donner le domaine de définition de y.

2°) Calculer les limites aux bornes de l'ensemble de définition.

3°) Calculer sa fonction dérivée y'. On précisera en valeur exacte, les coordonnées des deux extremums locaux.

4°) Etudier la dérivabilité en x = 0⁺ et en conclure la 1/2 tangente en ce point.

5°) Calculer la dérivée seconde y''.

Montrer que le polynôme est factorisable par (2X-1) et en déduire les coordonnées exactes et approchées du premier point d'inflexion.

On précise que le deuxième point d'inflexion est d'abscisse 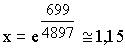et d'ordonnée .

6°) Dresser un tableau de variations complet. (On y précisera surtout les tangentes aux points particuliers).

7°) Tracer de façon soignée la fonction y = f(x) échelle 1 unité <=> 5 cm.

Partie B: (3 points)

On veut maintenant calculer l'aire et donc la primitive de y = f(x).

1°) Intégrer 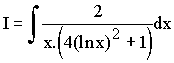en utilisant le changement de variable u = lnx.

2°) Calculer alors .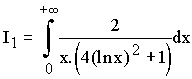

Partie C: ( 3 points)

Soit y = g(x) = Arctan[ln (x²)].

1°) Donner le domaine de définition de y = g(x) ainsi que le domaine d'étude (parité).

2°) Calculer les limites en +¥ et en o⁺, conclure.

3°) Calculer y' = g'(x).

4°) En déduire une étude sommaire de y = g(x). On étudiera cependant la dérivabilité en 0⁺ et on en déduira la 1/2 tangente en 0.