On considère l’application f de R³ dans R³ dont la matrice dans la base est

A = .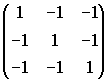

1° Démontrer que dans ce cas , il existe deux valeurs propres l ₁ et l ₂ que l’on déterminera (avec l ₁ < l ₂ ).
Déterminer le vecteur propre associé à l ₁ , préciser l’ensemble E₁ ainsi obtenu.

Montrer que l’ensemble obtenu pour la seconde valeur propre est un plan dont on donnera l’équation .

Donner deux vecteurs ( et ) qui constitueraient une base de ce plan.

2° On désigne par I l’application identique de E. Préciser la matrice associée.

Vérifier que les vecteurs , et sont des vecteurs propres de A.

Déterminer l’image de ces vecteurs par l’application f - I.

Montrer que la famille est une base de R³ .

Quelle est dans cette nouvelle base la matrice M semblable à A ?

3° Montrer matriciellement que f ² = f o f et f ³ = f ² o f sont des combinaisons linéaires de f et de I.

Plus généralement montrer par récurrence que f ⁿ = a _n . f + b _n . I n Î N^* .

Application: Déterminer n tel que f ⁿ = 21.f + 22.I

TRANSFORMEE DE FOURIER:

Donner la transformée de Fourier de la fonction f(t) représentée;e ci-dessous:

En déduire la transformée de g(t) représentée ci-dessous:

Peut-on retrouver la transformée de g(t) à l'aide du formulaire ?

FONCTIONS A PLUSIEURS VARIABLES:

Soient les équations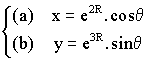

où x et y sont des variables indépendantes. C’est à dire, par exemple, que la dérivée de x par rapport à x vaut 1 et la dérivée de y par rapport à x vaut 0.

1° Dériver les deux équations par rapport à x. On obtient deux équations à deux inconnues ( et ). Résoudre ce système.

2° Dériver les deux équations par rapport à y. On obtient deux équations à deux inconnues ( et ). Résoudre ce système.

Retourner à la liste des contrôles

Retourner à la page d'accueil