Exercice 1:(5 pts)

Soit l’équation (E) .

Intégrer l’équation en utilisant le changement de variables

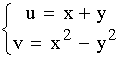
Exercice n°2: (5 pts)

Calculez l’original de F(z) = .

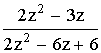Vérifiez le théorème de la valeur initale et , si c’est possible, celui de la valeur finale.

Problème:(10 pts)

Soit la matrice [A] = .

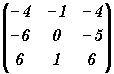Partie 1: (5 pts)

a) Déterminer l’équation caractéristique notée D(l).

b) Déterminer les valeurs propres de la matrice qu’on notera

l ₁, l ₂, l ₃ dans l’ordre croissant.

c) Déterminer les vecteurs propres associés.

d) Donner l’expression de la matrice [D] et de la matrice de passage

[P] de l’ancienne base à la nouvelle base .

Partie 2: (5 pts)

a) Calculer dét[P].

b) Calculer [P]^-1.

c) Sans exprimer [A]ⁿ , ni [D]ⁿ , démontrer par récurrence que:

( )

vecteurs propres .

d) Calculer [D]ⁿ ( ).

e) Calculer [A]ⁿ ( ).