Le 21 novembre 1998 Ni documents ni calculatrice graphique.

Exercice n°1:(3 points)

Soit l'équation (E) :

Donner les solutions de cette équation sachant qu'une racine est une imaginaire pure.

Exercice n°2: (2 points)

Calculer la limite suivante:

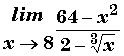
Exercice n°3: (7 points)

On veut placer sur le plan de Gauss (le plan complexe) les solutions de (E) :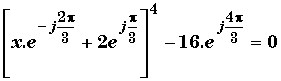

1. Résoudre et montrer graphiquement en les plaçant que les racines Z_k forment un carré.
2. Exprimer x en fonction de Z. Expliciter les deux transformations géométriques successives qui permettent de passer de Z à x.
3. En s'appuyant sur un graphique, donner alors les quatre solutions x_k .

Exercice n°4: (2 points)

Calculer la dérivée nième de

Exercice n°5: (6 points)

Dans une feuille carrée de côté a , on veut former une boîte fermée de longueur y, de largeur x et de hauteur z (voir schéma).

1. Exprimer le volume V de la boîte en fonction de z.
2. Calculer et donner alors l' intervalle dans lequel se situe z (pour lequel le volume est positif J ).
3. Résoudre =0 et donner la valeur du volume pour ces solutions.
4. Esquisser le tracé de V=f(z) dans l'intervalle précédent. Quelles sont les valeurs de x, y, z et V pour obtenir un volume maximal ?