|
|
|
tutorés |
de réflexion |
|
|
Devoir surveillé GTR1 n°3 M Sokol
Sans documents ni calculatrices graphiques
2 heures au 24 Avril 1999
Exercice 1: A propos du produit de convolution
On rappelle la définition du
produit de convolution: f(t) *
g(t) = 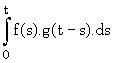
Soit l'équation différentielle,
![]() dans
laquelle f est une fonction continue du temps. En utilisant la méthode
de la variation de constante montrer que la solution peut s'écrire y(t)
=
dans
laquelle f est une fonction continue du temps. En utilisant la méthode
de la variation de constante montrer que la solution peut s'écrire y(t)
= 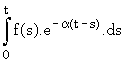 , c'est
à dire y = f *
h avec h(t) =
, c'est
à dire y = f *
h avec h(t) = ![]() .
.
Expliciter y(t) si f(t) = u (t) (l'échelon unité)
Exercice 2: LES BERNOULLI
1. Daniel Bernoulli
Dans la seconde génération des Bernoulli, Daniel (1700-1782) fut sans doute le plus important. Après des études médicales, il passa sept ans, de 1726 à 1733, à l’Académie de Saint-Pétersbourg en tant que mathématicien; après son retour à Bâle, il fut successivement professeur de botanique, d’anatomie et de physique.
À partir de considérations purement mathématiques, il a exp osé dans son ouvrage Hydrodynamica
&n bsp;paru en 1738 les premiers principes de ce qu’on appelle de nos jours la théorie cinétique des gaz, qui consiste à interpréter la pression d’un gaz comme provenant du choc des molécules gazeuses; dans le même ouvrage, il montre le rôle fondamental du principe de conservation de l’énergie en hydrodynamique. Daniel Bernoulli étudia également les cordes vibrantes et on peut le considérer comme un des fondateurs de la physique mathématique.2. Aperçu historique
Quoique certaines sommes de séries tr igonométriques aient déjà été calculée s par L.
Euler (cf. anal yse HARMONIQUE), on peut considérer que l’histoire des sériess trigonométriques remonte à la solution, donnée par D. Bernoulli, du problème des cordes vibrantes . Le problème est de calculer (cf. figure) le mouvement d’une corde, de longueur l , fixée en ses extrémités, et qui est soit écartée de sa position d’équilibre et lâchée (corde de guitare), soit frappée de façon à lui imprimer, en ses différents points, des vitesses de déplacement latéral (corde de piano).L’équation des cordes vibrantes, qui concerne le déplacement latéral y
(x , t ) (supposé petit) au temps t du point x de la corde, est: les conditions initiales imposent:
![]()
et respectivement:
![]()
pour la corde pincée, et:
![]()
pour la corde frappée. D’Alembert et Euler avaient découvert la solution générale, sous la forme:
![]()
où f
est une fonction périodique et de période 2 l qui, dans le premier cas, est impaire et égale à f/2 sur [0, l ] et, dans le second cas, est paire et primitive de q/2 y sur [0, l ]. Pour des raisons physiques évidentes, D. Bernoulli pensait pouvoir écrire la solution sous la forme d’une série d’harmoniques solutions de l’équation des cordes vibrantes, c’est-à-dire: dans le premier cas et, dans le second cas,
![]()
© 1998 Encyclopædia Universalis France S.A.Tous droits de propriété intellectuelle et industrielle réservés.
Considérons donc l'équation de Bernoulli:
![]() (
a¹1)
(
a¹1)
Montrer qu'en posant ![]() , on obtient une équation linéaire du premier ordre.
, on obtient une équation linéaire du premier ordre.
En prenant a(x) = 2, b(x) = 1, f(x) = x² et a = 3, intégrer alors l'équation et présenter la solution y(x)
Exercice 3: Une intégration classique
Soit la fonction ![]()
1) Calculer sa dérivée.
2) Donner l'allure de f(x) entre o et +¥
3) Intégrer ![]()
Rappel: ![]()
Exercice 4: A propos des équations différentielles du second ordre
Intégrer x.y' + 2.x – y = 0
Exercice 5: Sur l'intégration des fonctions rationnelles
Intégrer ![]()