tutorés |
de réflexion |
Episode 3
: Analyse combinatoire
L'analyse combinatoire comprend un ensemble de méthodes qui permettent de déterminer le nombre de tous les résultats possibles d'une expérience particulière.
Exemple: Un système d'immatriculation comprend 4 chiffres dont le premier est distinct de 0 et de 2 lettres distinctes de I et O et différentes. Le nombre de plaques est n = 9x10x10x10x24x23 = 4 968 000.
I ARRANGEMENTS
1) Définition
On appelle arrangement de n éléments
p à p (![]() ), tout ensemble
ordonné de p de ces éléments, tous distincts. Un arrangement est donc
caractérisé par la nature des éléments ou par leur ordre.
), tout ensemble
ordonné de p de ces éléments, tous distincts. Un arrangement est donc
caractérisé par la nature des éléments ou par leur ordre.
Calcul de ![]() :
:
|
1 |
2 |
p–1 |
p |
Dans la première case, on peut placer un objet parmi n, dans la deuxième, un objet parmi n–1 et ainsi jusqu'à la p-ième où on peut placer un objet parmi n–p+1.
D'où ![]() = n.(n–1)
(n–2)…(n–p+1)
= n.(n–1)
(n–2)…(n–p+1)
Exemple: Tiercé dans l'ordre dans une course de 14 chevaux.
![]() = 14x13x12 = 2184.
= 14x13x12 = 2184.
Avec la notation factorielle, ![]() s'écrit:
s'écrit: ![]() =
=
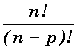
2) Arrangement avec répétition
Un arrangement de en objets p à p avec
répétition est un arrangement où chaque objet peut être
répété jusqu'à p fois d'où
![]()
II PERMUTATIONS
1) Définition
Une permutation de n objets est un ensemble ordonné de ces n objets. Les permutations de ces n objets constituent un cas particulier des arrangements. C'est le cas où n = p. Deux permutations ne diffèrent que par l'ordre des objets.
Calcul de ![]() .
.
Exemple: Nombre de configurations possibles à
l'arrivée d'une course de 8 chevaux ![]()
2) Permutation avec répétitions
Il arrive que, parmi les n objets dont on cherche le nombre de permutations, certains d'entre eux, au nombre de r, soient tous semblables. Auquel cas, rien ne distingue les permutations de ces r objets entre eux.

Généralisation: Soient r1 objets
semblables entre eux, r2 objets semblables entre eux, …, rk objets
semblables entre eux avec r1 + r2 +…+ rk = n, alors la
permutation devient: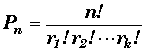 .
.
Exemple: Nombre de permutation possibles avec les lettres du mot indienne.
![]()
3) Permutation circulaire
Le rangement de 4 objets fournit 4! = 24 permutations différentes mais le rangement de ces 4 objets sur un cercle ne fournit plus que 6 permutations différentes.
Généralisation: n objets peuvent être disposés sur un cercle de (n–1)! manières différentes, soit le nombre de permutations Pn divisé par le nombre de manières différentes de choisir la première place.
III COMBINAISONS
1) Définition
On appelle combinaison de p éléments pris parmi
n (![]() ), tout ensemble que l'on peut former en
choisissant p de ces éléments, sans considération d'ordre.
), tout ensemble que l'on peut former en
choisissant p de ces éléments, sans considération d'ordre.
Deux combinaisons distinctes diffèrent donc par la nature d'au moins un élément.
Exemple: Les combinaisons possibles de 4 lettres A B C D, 3 à 3 sont A B C, A B D, A C D, et B C D.
Calcul de ![]()
On peut remarquer qu'un arrangement de n objets p à p
n'est autre que le produit d'une combinaison de n objets p à p par le nombre
de permutations de ces p éléments: ![]() =
=![]() .
.![]()
D'où ![]() =
=
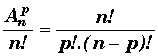
Remarque: ![]() et
et ![]()
Exemple: Nombre de tiercé dans désordre dans une
course de 14 chevaux: ![]()
2) Binôme de Newton
Le binôme de Newton est le produit de n facteurs égaux
à ( a+ b ) d'où 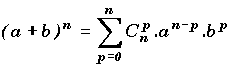 .
.
Les ![]() sont
déterminés au moyen du triangle de Pascal.
sont
déterminés au moyen du triangle de Pascal.
3) Combinaison avec répétitions
Supposons que l'on étudie la répartition de n objets en fonction de r critères, et que l'on cherche le nombre de telles répartitions possibles.
Une telle répartition est appelée combinaison avec
répétition , son nombre est ![]() .
.
Soient x1 , x2 , … , xn objets qu'on sépare par r frontières
![]()
Le nombre de combinaisons avec répétition est donc égal au nombre de manières de séparer les xi par r frontières. C'est donc le nombre de manières de choisir r objets parmi n + r – 1 sans tenir compte de l'ordre.
Exemple: Lors d'un sondage dans une université on pose à 100 étudiants 1 question comportant 3 réponses possibles. Quel nombre de configurations différentes peut-on obtenir?
N = 100 r=3 ![]()