tutorés |
de réflexion |
FONCTIONS LOGARITHMES
ET EXPONENTIELLES
I Situation
L’entreprise Lartronic S.A conçoit et commercialise des filtres passifs électroniques (Passe-bas , passe-haut et passe-bande). Ils se présente sous forme de circuits intégrés pouvant contenir de 2 à 4 filtres. Hormis leur catalogue, le client peut demander du "sur mesure" en donnant ses fréquences de coupure.
Il est donc nécessaire pour la conception de maîtriser les fonctions logarithmiques.
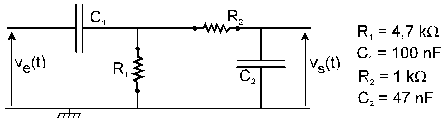
Illustration 1 : Filtre passe-bande

Illustration 2 : Modélisation d’un filtre
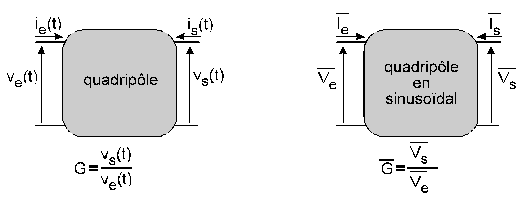
Illustration 3 : Expression du gain
********************************************
De plus, nous avons vu dans le chapitre sur les complexes, que la notation exponentielle était la plus usité. Nous verrons ultérieurement que dans les mathématiques du traitement du signal elles seront encore présentes (Transformées de Laplace, transformées de Fourier).
II Fonction logarithme népérien
On appelle logarithme népérien, noté ln ou Log, la
primitive de la fonction ![]() pour x>0 et s’annulant pour x = 1.
pour x>0 et s’annulant pour x = 1.
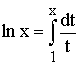
Remarque épistémologique: Les deux fonctions logarithmes les plus utilisées sont celles à base e = 2,71828…. et à base 10 . On les appelait respectivement autrefois le grand log (Log)et le petit log (log). Aujourd’hui, logarithme népérien (ln) et logarithme à base 10 (log)
2-a) Propriété fondamentale
![]()
![]()
![]()
Démonstration :
Considérons la fonction ln (a.x)
Sa dérivée est
![]() .
.
Si on intègre cette égalité on obtient ln(a.x) = lnx + C
En posant x = 1 , et à l’aide de la définition on obtient que lna = C
Et en posant enfin x = b
![]()
2-b) Conséquences
![]()
![]()
![]()
![]()
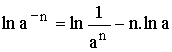
* En l’infini
![]() et x>1 est toujours
comprise entre 2 puissances successives de a :
et x>1 est toujours
comprise entre 2 puissances successives de a :
![]()
![]()
comme ![]() alors
alors
![]() donc
donc
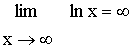
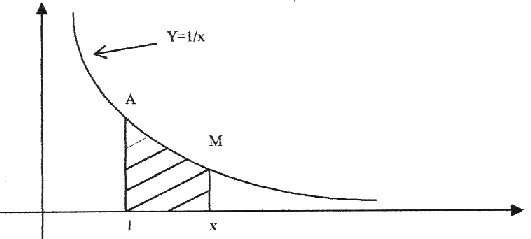
Recherchons maintenant
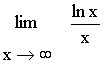
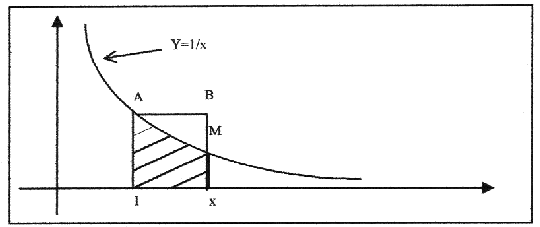
D’après le graphique, il est évident que lnx est inférieur au rectangle (1,x,B,A)
Démonstration :
![]()
![]()
![]()
![]()
![]()
![]()
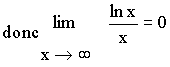
L’axe Ox est donc Branche Parabolique de Direction Asymptotique .
![]() Plus généralement,
on retiendra
Plus généralement,
on retiendra
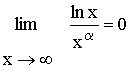 avec
avec
![]()
* En zéro
Dans la recherche de
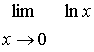 ,
posons
,
posons ![]() ce qui nous permet
ce qui nous permet
d’écrire :
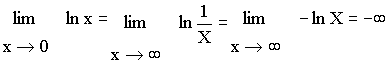
La courbe possède donc une asymptote verticale en x = 0.
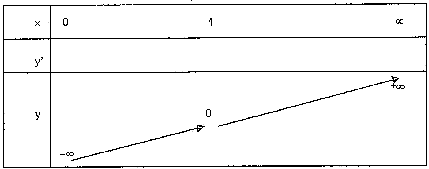
On remarque que pour x = 1 , y = 0 , y’(1) = 1
Pour x= e » 2.71828 , y = 1
La dérivée seconde
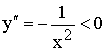 nous donne une concavité toujours tournée vers les y
négatifs.
nous donne une concavité toujours tournée vers les y
négatifs.
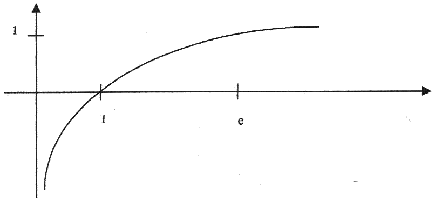
4-a) On remarque que la fonction g(x) = ln(1 + x) est dérivable en zéro, son calcul
nous donne
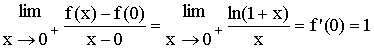 .
.
Ce qui nous permet d’écrire l’infiniment petit :
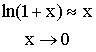
4-b) Calculons la dérivée de y = ln|x|
si x>0 Þ
y = lnx Þ
y’= ![]()
si x<0 Þ
y = ln(–x) Þ
y’ = ![]()
alors on retiendra
![]() ou
encore
ou
encore 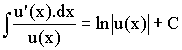 où u(x) est
une fonction de x.
où u(x) est
une fonction de x.
III Fonction logarithme de base a
On appelle logarithme de base a, notée
![]() , la fonction définie par
, la fonction définie par
![]()
![]()
![]()
Regardons la variation de cette courbe en calculant la dérivée
![]()
Donc si ![]()
![]()
![]()
Et si ![]()
![]()
![]()
On peut aussi remarquer
![]()
![]()
D’ou les courbes
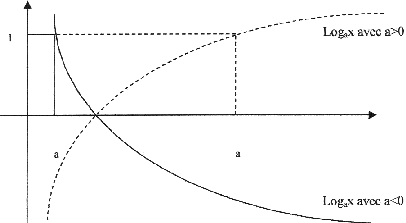
Il est très utile de passer d’un logarithme à une
base a donnée à un logarithme d’une autre base
b par exemple. Le cas le plus connu pour les scientifiques
étant le passage du logarithme népérien au
logarithme de base 10 (![]() noté maintenant log x) dont la réciproque, que nous
définirons après, est
noté maintenant log x) dont la réciproque, que nous
définirons après, est
![]() utilisée
dans tous les domaines de la physique et de la chimie.
utilisée
dans tous les domaines de la physique et de la chimie.
Soit donc b une nouvelle base.
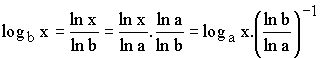
D’où la formule du changement de base
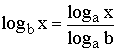
Cas particulier à retenir : a = e et b = 10
![]()
D’où ![]() et inversement
et inversement ![]()
IV Fonction exponentielle
Les fonctions
![]() sont continues et
monotones pour x>0. Elles réalisent de ce fait une
bijection de R*+ sur R et sont donc inversibles. Leurs
fonctions réciproques sont appelées exponentielles de
base a et notée expa et sont définies
sont continues et
monotones pour x>0. Elles réalisent de ce fait une
bijection de R*+ sur R et sont donc inversibles. Leurs
fonctions réciproques sont appelées exponentielles de
base a et notée expa et sont définies
par ![]() ou
ou
![]()
Ces fonctions sont continues et monotones pour tout x et
établissent une bijection de R sur R*+ avec
![]()
![]()
Les points particuliers sont définis par :
![]()
![]()
On notera les deux fonctions exponentielles essentielles
![]() et
et
![]()
2-a) Relation fondamentale
![]()
![]()
![]()
entraîne
![]()
ou
![]()
2-b) limites comparées
![]() Nous avons vu précédemment que " Puissance l’emporte
sur logarithme ", on retiendra de la même façon
que " exponentielle l’emporte sur puissance "
Nous avons vu précédemment que " Puissance l’emporte
sur logarithme ", on retiendra de la même façon
que " exponentielle l’emporte sur puissance "
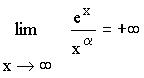 avec
avec
![]()
V Fonctions exponentielles généralisées
Ce sont des fonctions dont la présentation est de la même forme qu’une exponentielle ou une fonction puissance, mais où u(x) et v(x) sont des fonctions de x.
![]()
Il est cependant impossible d’étudier ces fonctions telles qu’elles se présentent. Il faut revenir à une notation exponentielle classique.
![]()
![]()
On retiendra cette dernière expression.
VI Echelle logarithmique
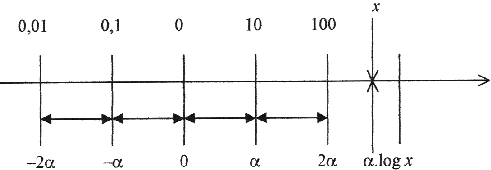
Lorsqu’on étudie un phénomène représenté par une fonction f(x) sur une gamme étendue de valeurs de x, l’échelle linéaire pour les abscisses est mal adaptée. On lui préfère une échelle logarithmique, en général de base 10. Elle permet de " dilatée " les faibles et les fortes valeurs.
En appelant a la distance entre les extrémité d’une décade (dizaine), on place x sur l’échelle logarithmique à l’aide de son représentant a .log x . Ce qui nous donne :
VII Le Décibel (dB)
Dans les disciplines de l’électricité (électronique,
électrotechnique, automatique ,…), on est amené à faire
l’étude des systèmes linéaires nécessite le calcul
du module d’une fonction de transfert, de la forme
![]() . On exprime ce
module en décibel à l’aide de la relation :
. On exprime ce
module en décibel à l’aide de la relation :
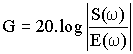 et est appelé gain. w
est la pulsation (w
³
0)
et est appelé gain. w
est la pulsation (w
³
0)
Prenons en exemple le cas d’un système du premier ordre :
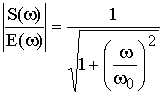
D’où le gain G exprimé en dB :
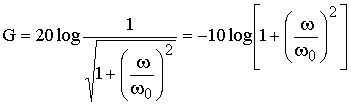
Prenons quatre valeurs particulières :
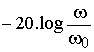
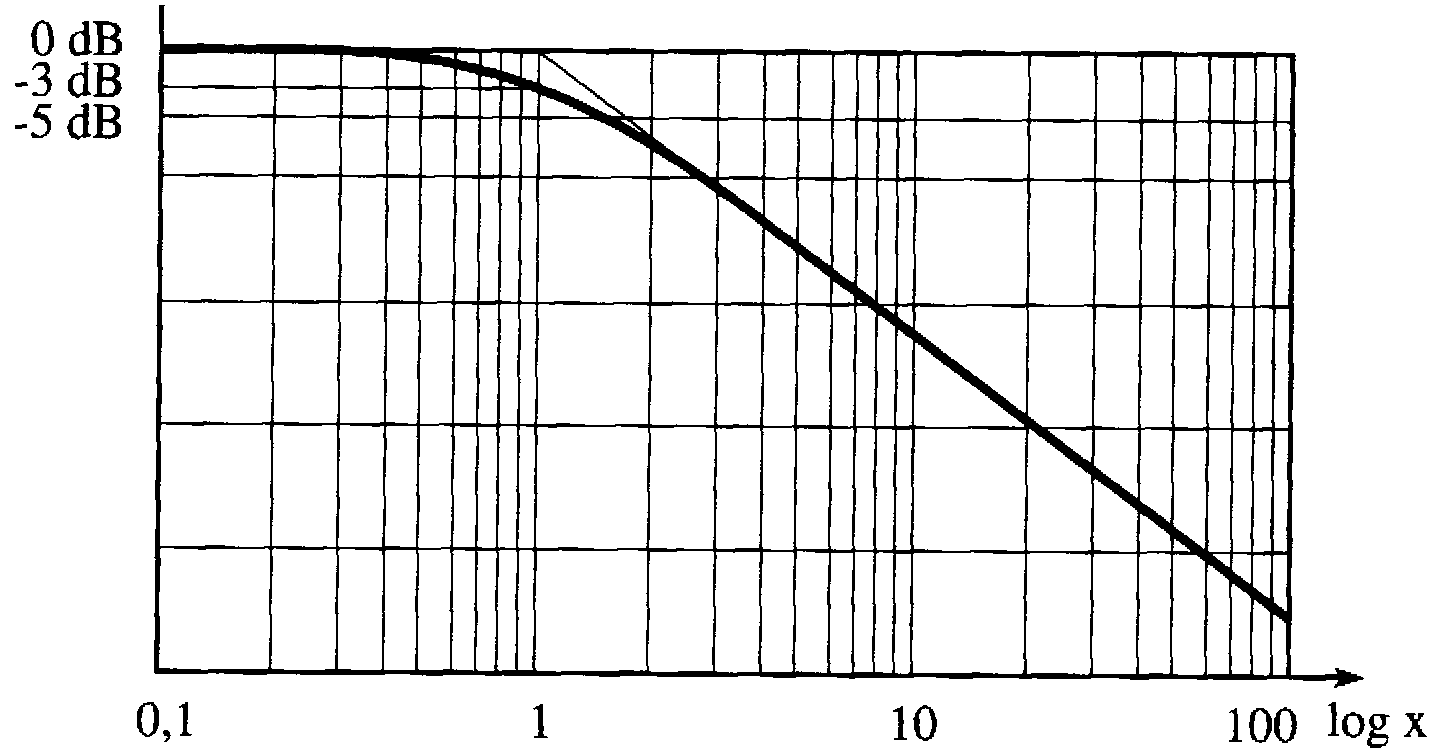
On remarque ainsi que pour les grandes valeurs de w la courbe représentative de G en échelle logarithmique admet donc pour asymptote une droite dont la pente par décade est
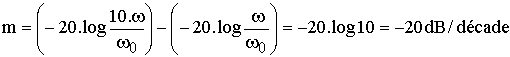
Ci-dessous seront tracées trois courbes :
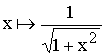 , en échelle
linéaire pour x =
, en échelle
linéaire pour x =
![]()
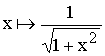 , en échelle
logarithmique pour x
, en échelle
logarithmique pour x
![]() ,
en échelle logarithmique pour x
,
en échelle logarithmique pour x
On observe que la courbe 1 est peu lisible pour les petites et grandes valeurs de x. Par contre les courbes 2 et 3 sont exploitables pour toutes les valeurs de x . On remarque de plus que la courbe 3 fait apparaître l’asymptote G = –20.log x
Figure 1

Figure 2
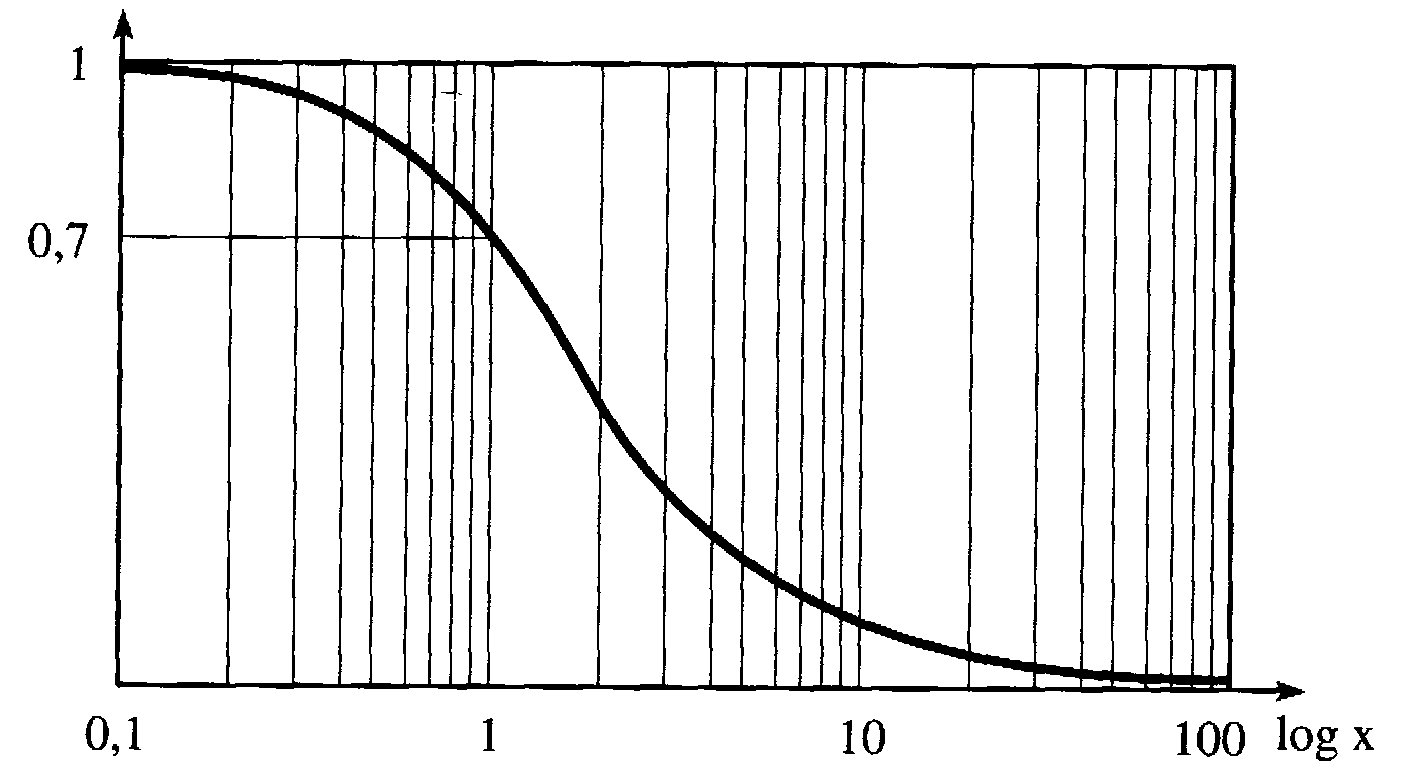
Figure 3