tutorés |
de réflexion |
Transformation de Laplace
I Définition
Soit f une fonction de la variable réelle t, définie sur R et supposée nulle pour t négatif (
fonction causale)On appelle transformée de Laplace de f, la fonction F définie par:
Où p est une variable complexe.
On écrit :
F(p) = L [f(t)] ou F(p) Ì f(t)
f(t) = L–1 [F(p)] ou f(t) É F(p)
La transformée de Laplace d'une fonction n'existe que si l'intégrale est convergente, pour cela on est amené à imposer à f deux conditions :
* être continue par morceaux sur tout fermé [0 ; x0 ]
* être "d'ordre exponentiel à l'infini", c'est à dire qu'il existe M>0 et a tels que |f(t)|<Mea .t pour t > X.
On démontre que si les hypothèses précédentes sont vérifiées, la transformée de Laplace est définie pour p>a , ou si p est complexe, pour  (p) > a .
Le domaine de convergence de F(p) est ]
a
; ¥
[ (a
Î
R) ou encore, le ½ plan complexe Â
(p) > a
(a
Î
C).
Par la suite on considérera en général que  (p) > 0.
II Transformée de fonctions élémentaires
II-1 Fonction échelon unité (fonction d'Heaviside) U(t)
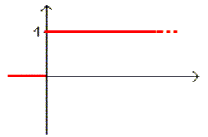
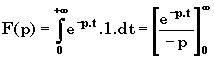Si Â
(p)>0 alors 
ce qui implique
II-2 Fonction impulsion unité (Distribution de Dirac)
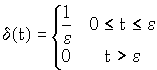
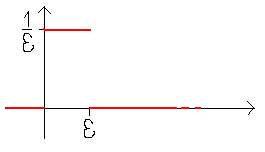
Remarque:
" e , on a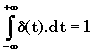
.
Si e
tend vers 0, la distribution de Dirac qui n'est pas une fonction sert à
représenter en physique une action s'exerçant sur un instant
très court (impulsion)
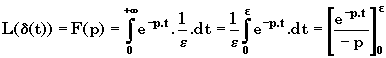avec
Â
(p)>0
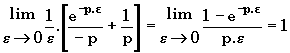(on utilise les développements limités ou la règle
de l'Hospital)
II-3 Fonction puissance
Soit
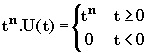( n Î N ). Calculons donc
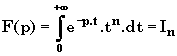
Posons le changement de variables :
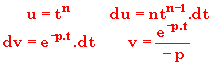
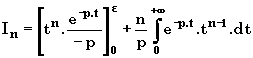(le premier crochet est nul si Â
(p)>0 )
D'où 
;
;
; ... ... ...
II-4 Fonction exponentielle
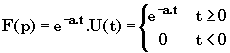
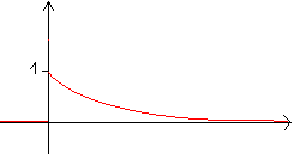
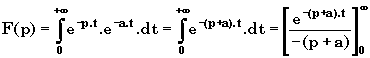
Si Â
(p + a) > 0 alors,
, d'où
III Propriétés
III-1 Linéarité
" a et " b Î C et L[f(t)] = F(p) et L[g(t)] = G(p)
| L[a .f(t) + b.g(t)] = a . F(p) + b. G(p) |
Exemple
: Transformée de Laplace de cos w t.U(t) et sinwt.U(t)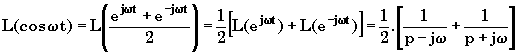
d'où
De même pour sinwt :
III-2 Règle de similitude (Changement d'échelle)
Soit g(t) = f(at) ( a>0 )
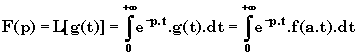
On pose alors le changement de variables :
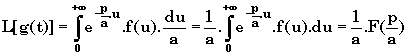
III-3 Règle de translation en p:
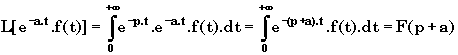
Exemple:
III-4 Règle de translation en t
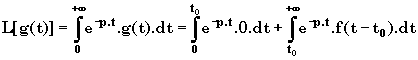
On pose
u = t – t0 et du = dt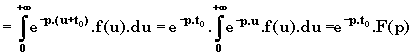
est appelé
facteur retard
Exemple:
Image d'un créneau entre 0 et t0 .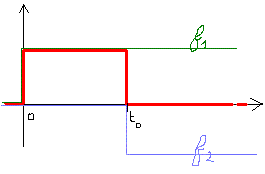 | f(t) = f1(t) + f2(t) = U(t) – U(t – t 0)  , d'où
 |
Application:
Transformée d'une fonction périodique.
Soit f une fonction périodique pour t>0 de période T
En appliquant la linéarité et le théorème du retard
Il suffit de connaître la transformée de F0(p) de la fonction f0 qui coïncide avec f sur [ 0 ; T ].
III-5 Transformée de la dérivée.
Théorème fondamental :
Si f' est continue par morceaux sur tout fermé [0; x0] et si alors
En effet
En intégrant par parties, on obtient:
Comme
f(0+ ) représentant la limite à droite de f(t) quand t –> 0, d'où le théorème
Généralisation: Si f'' vérifie à son tour les hypothèses du théorème, on a:
"Dériver c'est multiplier par p"
Cette propriété, qui fait la richesse de la transformée de Laplace sera largement utilisée dans les équations différentielles
Remarque importante :
Théorème de la valeur initiale:
Théorème de la valeur finale:
III-6 Transformée de la primitive
Théorème:
Si
En effet
En appliquant le théorème de la dérivée
Par ailleurs
( n Î
N)
(
Â
(p) > –Â
(a) )
