tutorés |
de réflexion |
Exercice :
Calculer:
S = ![]() et S' =
et S' =
![]()
(On pourra utiliser S + i.S')
Exercice :
Transformer en un produit les expressions:
cos(a + b + c) + cosa + cosb + cosc ;
sin(a + b – c) + sin(b + c – a) + sin(c + a – b) – sin(a + b + c)
Exercice :
En supposant a + b + c = p , simplifier les expressions:
![]() ;
;
1 + cosa + cosb + cosc
Exercice :
Démontrer que
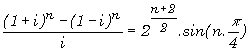
Exercice :
Dans le corps des complexes,
résoudre l'équation
![]() , où z
est l'inconnue et
, où z
est l'inconnue et ![]() le conjugué de z
le conjugué de z
Problème :
Un peu d'histoire
:Cardan (Gerolamo Cardano en fr: jérôme), mathématicien, médecin et philosophe italien, né à Pavie (1501-1576). Il généralisa et développa la résolution des équations du 3ème degré et imagina le mode d'articulation qui porte son nom.En étudiant l'équation du troisième degré
x3 + px = q; Cardan trouve, lorsque p est positif, la racine
réelle de cette équation sous la forme :
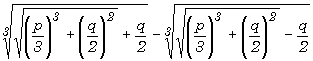
Retour vers le présent:
1°) Soit l'équation a.x3 + b.x2 + c.x + d = 0 , où a, b, c, et d sont des nombres complexes tels que a ¹ 0.
On pose ![]() .
.
Montrer qu'on se ramène à la résolution d'une équation du type z3 + p.z + q = 0 (E1), où p et q sont des nombres complexes.
Montrer que l'équation E1 admet au moins une racine réelle lorsque p et q sont réels.
2°) z étant un nombre complexe satisfaisant E1, on pose z = u + v, avec 3uv + p = 0. Montrer que u3 et v3 sont les racines y1 et y2 d'une équation du second degré que l'on formera. Comment faut-il associer les racines cubiques de y1 et y2 pour que leur somme soit racine de E1?
Effectuer les calculs lorsque p et q sont réels (distinguer les cas 4p3 + 27q2 > 0
et 4p3 + 27q2 < 0).
Retrouver les formules de Cardan ci-dessus.
Résoudre sur C les équations x3 – 2x – 12 = 0 et x3 – 15x – 4 = 0.
3°) a
, b
et g
désignant les racines de E1, démontrer que z =
(a
+ b
.j + g
.j²)3 ,où ![]() ,
ne prend que deux valeurs z1 et z2
lorsque l'on permute a
, b
et g
de toutes les manières possibles.
,
ne prend que deux valeurs z1 et z2
lorsque l'on permute a
, b
et g
de toutes les manières possibles.
Former l'équation du second degré admettant z1 et z2 pour racines. En déduire une méthode de résolution de E1. Effectuer les calculs lorsque p et q sont réels.
4°) a) En exprimant cos3a en fonction de cosa , montrer que l'équation cos3a = a se ramène à une équation du troisième degré du type x3 + px + q = 0, avec 4p3 + 27q2 < 0, lorsque l'on suppose |a|<1.
b) Réciproquement, étant donnés deux réels p et q tels que 4p3 + 27q2 < 0, montrer qu'il existe des réels r et j tels que E1 admette pour racines : r cosj, r .cos(j + 2p /3), r.cos(j + 4p/3). Calculer r et cos 3j en fonction de p et q.
Résoudre sur C l'équation x3 – 4x + 1 = 0.