COMPLEXES II

Complexe ou compliqué II
Exercice 1: Calculez les racines carrées, en notation algébrique, de
z₁ = – .j
z₂ = 2j
z₃ =– 3 + 4j
z₄ = –12 – 5j
Exercice 2: Factorisez dans l'ensemble des complexes C :
P₁(z) = z² – 2z + 10

P₂(z) = z² – 2.(3 + 2j).z + 10

P₃(z) = 2z² – (4 + 5j).z + 3.(1 + 4j)

P₄(z) = j.z² + j.z + j + 1
Exercice 3:
Factorisez le polynôme suivant sachant qu'il a une racine réelle.
P(z) = 2z³ –(1 + 10j).z² – (11 – 7j).z + 12.(1 + j)
Exercice 4:
Factorisez le polynôme suivant sachant qu'il a une racine imaginaire pure.
P(z) = z³ – 3j.z² + (5 – 3j).z –4.(3 + j)
Exercice 5: Soit le dipôle suivant :

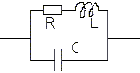
1) Calculez l'impédance équivalente.

2) Calculez le module et l'argument j .

3) Calculez la valeur de C qui annule le déphasage
(c'est à dire résoudre tanj = 0).

4) Application numérique: R = 1kW ; L = 0,15 H et w = 314 rad/s
Exercice 6: Soit le dipôle suivant :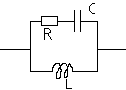

1) Calculez l'impédance équivalente.

2) Calculez le module et l'argument j .

3) Donnez une approximation du module et de l'argument quand w ® 0

4) Donnez une approximation du module et de l'argument quand w ® ¥
Exercice 7: Soit le dipôle suivant :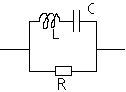

1) Calculez l'impédance équivalente.

2) Calculez le module et l'argument j .

3) Donnez une approximation du module et de l'argument quand w ® 0

4) Donnez une approximation du module et de l'argument quand w ® ¥
Exercice 8: Soit le dipôle suivant :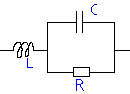

1) Calculez l'impédance équivalente.

2) Calculez le module et l'argument j .

3) Donnez une approximation du module et de l'argument quand w ® 0

4) Calculez la valeur de L qui annule le déphasage
(c'est à dire résoudre tanj = 0).

5) Application numérique: R = 1kW ; C = 470nF et w = 2000p rad/s
Exercice 9: Soit le dipôle suivant :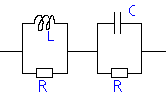

1) Calculez l'impédance équivalente.

2) Calculez le module et l'argument j .

3) Donnez une approximation du module et de l'argument quand w ® 0

4) Calculez la valeur de C qui annule le déphasage
(c'est à dire résoudre tanj = 0).

5) Application numérique: R = 660 W ; L = 0,1 H et w = 4000p rad/s