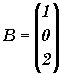
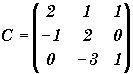 et
et
tutorés |
de réflexion |
Calcul matriciel
Déterminant 1
Exercice 1:
Soient les matrices ![]()
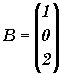
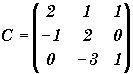 et
et
![]()
1) Si les produit sont possibles, effectuer A´
B, A´
C, A´
D, B´
C, C
´
B,
D
´ C, A´
D´
C, sinon préciser pourquoi.
2) Donner At , B t, C t et D t .
3) Calculer les déterminants respectifs
Exercice 2:
Les matrices suivantes sont-elles inversibles (on justifiera):
![]()
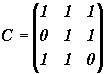
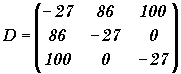
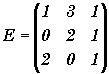
Exercice 3:
Si ![]() et
et
![]() , existe-t-il des matrices
A telles que A
, existe-t-il des matrices
A telles que A
Exercice 4:
Soit la matrice 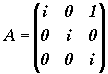 .
Calculer An (n
.
Calculer An (n
Exercice 5:
Calculer l'inverse de la matrice
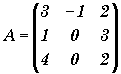 par la méthode du pivot de Gauss
par la méthode du pivot de Gauss
Exercice 6:
Résoudre, par la méthode du pivot de Gauss, le
système
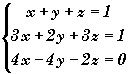 .
.
Exercice 7:
Soit u l'endomorphisme de R3
représenté
dans la base canonique par la matrice:
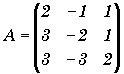
a) Calculer les valeurs propres de A.
b) Trouver une base de vecteurs propres.
c) Ecrire la matrice diagonale D de u dans la base B;
d) Calculer Dn , n
Î N*.e) En déduire An .