1°) Simplifier en donnant le domaine de définition:

sin ( 2 Arc sin x )	cos( 2 Arc cos x )	sin2 ( Arc cos x )
cos2 ( Arc cos x )	cos( Arc sin x + Arc sin y )	tan ( 2 Arc tan x )

2°) Vérifier que 2.Arc tan = Arc tan et 2 Arc cos = Arc cos .

3°) Calculer a = Arc tan + Arc tan .

4°) Résoudre:

5°) Résoudre:

6°) Soit S_n = .

6-a°) Montrer que S_n = . On utilisera un raisonnement par récurrence, puis on n' oubliera pas de vérifier la validité de S_n+1 .

6-b°) En déduire la limite

7°) Simplifier suivant les valeurs de x que l'on précisera

a) y = Arc tan ( tan x) b) y =

c) y = d) y = Arc cos ( 1 - 2x² )

8°) Montrer que " x Î [ -1;1] , Arcsin x + Arccos x = .

9°) Etudier, tracer, et simplifier la fonction: y = Arc sin ( 2 sinx cosx ).

10°) Calculer les dérivées de y = Arc tan et y = Arc tan

( On expliquera les résultats).

11°) Soit .

11-a°) Préciser le domaine de définition.

11-b°) Calculer y' et en déduire y ( on précisera la valeur de la constante).

11-c°) Calculer tany puis retrouver y.

12°) Soit y = .

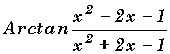12-a°) Donner l'ensemble de définition de y.

12-b°) Après avoir posé x = tan j , préciser l'ensemble de définition de
y = f(j ) (on remarquera tan(p /8) et tan(-3p /8)) et simplifier y = f(j ).

12-c°) Simplifier alors y = f(x).

13°) Soient quatre fonctions y₁ , y₂ , y₃ et y₄ .

13-a°) Etudiez et tracez les courbes représentatives puis simplifiez les expressions des deux premières fonctions:

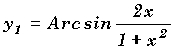
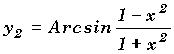
13-b°) A l'aide des simplifications précédentes, simplifier et tracer les deux fonctions suivantes:

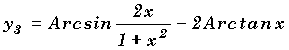
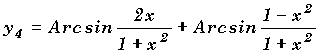
D D D Ñ Ñ Ñ D D D

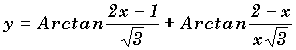Aller au cours de trigonométrie