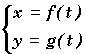 , pour toutes
les valeurs de
t, appartenant à Df
, pour toutes
les valeurs de
t, appartenant à Df
tutorés |
de réflexion |
Courbes en représentation paramétrée
I Définition
Soient f et g deux fonctions définies et continues respectivement sur les intervalles Df et Dg de R. Soit une variable réelle t.
Soit dans le plan rapporté à un repère
![]() le point M(x,y)
défini
par
le point M(x,y)
défini
par 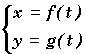 , pour toutes
les valeurs de
t, appartenant à Df
, pour toutes
les valeurs de
t, appartenant à Df
![]() Dg.
Dg.
L'ensemble des points M(x,y) définit une courbe dont le système
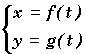 constitue la
représentation
paramétrique. La variable t est le paramètre.
constitue la
représentation
paramétrique. La variable t est le paramètre.
Remarque 1:
Une courbe dont on a la représentation paramétrée ne peut pas s'écrire forcément par une représentation cartésienne y = f(x), car à deux valeurs différentes du paramètre peuvent correspondre plusieurs points de même abscisse, ce qui interdit la notion de fonction.
Exemple: 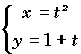
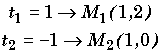
Remarque 2:
En éliminant le paramètre t entre x et y, on peut obtenir f(x,y)=0 .
Exemple: 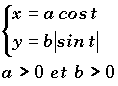
![]()
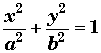
II Ensembles
II-1 Ensemble de définition
Il est obtenu par intersection des ensembles de définition de f(t) et g(t).
D = Df ![]() Dg
Dg
Exemple: 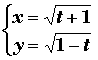 Df
= [-1,+µ
[ Dg = ]-µ
,1] d'où D = [-1,1]
Df
= [-1,+µ
[ Dg = ]-µ
,1] d'où D = [-1,1]
II-2 Ensemble utile
C'est l'ensemble des valeurs du paramètre par lesquels on obtient toute la courbe, une seule fois.
Exemple: 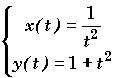 Si on remplace
t par -t, on obtient le même point ici Du = R+* .
Si on remplace
t par -t, on obtient le même point ici Du = R+* .
Théorème: Si les fonctions sont paires, ou le deviennent après un même changement de variable, on peut restreindre l'ensemble de définition à un ensemble utile.
Théorème: Si f et g sont périodiques de période Tf et Tg et s'il existe (a,b) Î N2* tel que a.Tf = b.Tg alors la période d'étude vaut T = a.Tf = b.Tg.
Exemple: 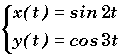
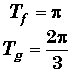 comme
2.Tf = 3.Tg
alors T = 2.p
comme
2.Tf = 3.Tg
alors T = 2.p
II-3 Ensemble d'étude
Il se déduit du domaine utile à l'aide de transformations géométriques simples (symétries ou translation).
II-3-1 Symétrie par rapport à 0x
Soit t1 Î
T1 et t2 Î
T2 avec t2 = j
(t1) si 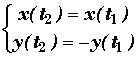 il y a symétrie par rapport à 0x.
il y a symétrie par rapport à 0x.
Exemple 1: 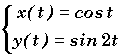 Du
= 2.p
comme t2 = j
(t1) = - t1 Þ
De = p
Du
= 2.p
comme t2 = j
(t1) = - t1 Þ
De = p
Exemple 2: 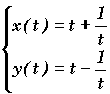 On remarque que
On remarque que 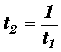 entraîne
entraîne
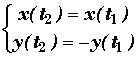 avec T1 = [-1,0[
È
]0,1] T2 = ]-µ
,-1]È
[1,µ
[
avec T1 = [-1,0[
È
]0,1] T2 = ]-µ
,-1]È
[1,µ
[
On peut prendre alors par exemple De = [-1,1]
II-3-2 Symétrie par rapport à 0y
De même si t1Î
T1 t2 Î
T2 et 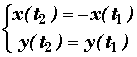 il y a symétrie par rapport à 0y
il y a symétrie par rapport à 0y
II-3-3 Translation
S'il existe un réel positif T tel que:
X(t +n.T) = x(t) + n.x(t)
y(t +n.T) = y(t) + n.y(t)
n Î Z
On peut alors réduire le domaine utile Du au domaine d'étude De = [t0,t0 + T].
Exemple: 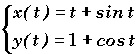 alors De = [0,2p
].
alors De = [0,2p
].
III Etude au voisinage d'un point
III-1 Point ordinaire
Le coefficient directeur de la tangente en (x0 ,
y0) pour t0 , est
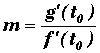 pour f'(t0) ¹
0 et si f'(t0) = 0 et g'(t0) ¹
0, la tangente est parallèle à l'axe 0y.
pour f'(t0) ¹
0 et si f'(t0) = 0 et g'(t0) ¹
0, la tangente est parallèle à l'axe 0y.
III-2 Point singulier
C'est un point pour lequel f'(t0) = g'(t0) = 0. On cherche alors m en effectuant les dérivées successives jusqu'à temps que f(n)(t0) ou g(n)(t0) ne soit pas nulle
D'où 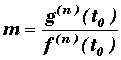 .
.
Exemple: 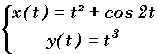 A
t0 = 0 M0 (1,0)
A
t0 = 0 M0 (1,0)
x'(t) = 2t - sin2t x'(0) = 0
y'(t) = 3t² y'(0) = 0
x''(t) = 2- 2cos2t x''(0) = 0
y''(t) = 6t y''(0) = 0
x'''(t) = 4sin2t x'''(0) = 0
x'''(t) = 6 y'''(0) = 6 On trouve donc ici que m ® µ
Remarque: En cinématique, les points singuliers sont appelés points stationnaires car leur vitesse est nulle.
IV Allure de la courbe au voisinage d'un point
IV-1 Si la tangente est parallèle à l'un des axes 0x ou 0y, la simple étude de f et g fourni l'allure de la courbe.
IV-2 Si la tangente est quelconque, on est amené à étudier le sens de variation de m:
IV-2-1 Si m varie dans le même sens de part et d'autre de M0(t0):
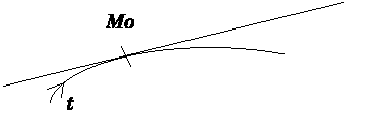

IV-2-2 Si m change de sens de variation de part et d'autre de M0(t0):

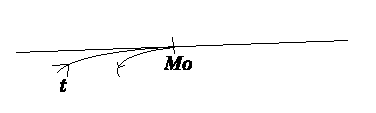
V Points multiples
La courbe présente un point double Md s'il existe deux valeurs t1 et t2 de l'ensemble utile Du telles que M(t1) et M(t2) sont confondus.
La recherche de ces points s'effectue en résolvant le système
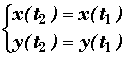 t1
¹
t2 sur Du
t1
¹
t2 sur Du
VI Branches infinies
VI-1 Définition
Une courbe admet une branche infinie lorsque t tend vers t0
ou l'infini si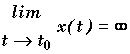 et /ou
et /ou 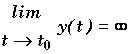
VI-2 Etude
* Si 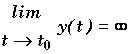 et
et
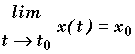 x = x0 est asymptote.
x = x0 est asymptote.
* Si 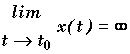 et
et
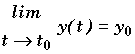 y = y0 est asymptote.
y = y0 est asymptote.
* L'étude est la même que pour les fonctions en menant
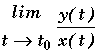 et
et
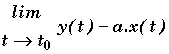 .
.
VII Résumé pour l'étude
3) Dresser la tableau suivant:
|
t |
|
|
f '(t) |
|
|
f (t) |
|
|
g (t) |
|
|
g '(t) |
|
|
m |
4) Précisez les points particuliers: stationnaires, multiples, d'inflexion et de rebroussement.
5) S'il y a lieu, étudier les branches infinies.
6) Tracé de préférence dans un repère orthonormé.