Exercice 1: Reconnaître les courbes définies par leurs équations paramétriques.

1) x(t) = a.t + a ; y(t) = b.t + b

2) x(t) = a. 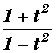; y(t) = b. ; a >0 ; b >0

Exercice 2: Voici la définition paramétrique des courbes C₁ , C₂ , C₃ et C₄. Tracer leur graphique et indiquer leur orientation.

Exercice 3: On considère la courbe C définie par les équations paramétriques: x(t) = sin3t et y(t) = sin4t.

Etudier et tracer cette courbe.

Exercice 4: Soit la courbe de paramétrisation x = t³ – 3t ; y = t² – 5t – 1

4-a Trouver une équation de la tangente à C , au point correspondant à t = 2.

4-b Pour quelles valeurs de t la tangente est-elle horizontale ou verticale ?

4-c Etudier et tracer cette courbe.

Exercice 5: Soit la fonction t ® j (t) = 3e^jt – e^3jt avec j² = –1

5-a Montrer que la fonction j est représentée dans un plan muni d'axes 0x et 0y par x = f(t) et y = g(t).

5-b A l'aide des symétries, montrer que le domaine utile D_U donne un domaine d'étude D_E de longueur p /2.

5-c Montrer que f'(t) = 6.sint.cos2t et g'(t) = 6.sint.sin2t

5-d Donner les tangentes aux points remarquables.

5-e Donner la tangente au point stationnaire

5-f Tracer la courbe C₁ liée au domaine d'étude puis la courbe utile C.

Remarque: La courbe est la trajectoire d'un point d'un cercle G ₂ de rayon 1 roulant sur un cercle G ₁ fixe de rayon 2. C'est une courbe cycloïdale. Les courbes cycloïdales interviennent en mécanique, notamment dans les profils d'engrenage et dans l'étude des mouvements plan sur plan. La courbe C appelée néphroïde est connue en optique; c'est la caustique d'un miroir sphérique concave (enveloppe des rayons lumineux réfléchis).