tutorés |
de réflexion |
EQUATIONS DIFFERENTIELLES DU SECOND ORDRE
I GENERALITES
On appelle équation différentielle du second ordre toute relation de la forme F(x,y,y',y'')=0 entre la variable x et la fonction y(x) et ses deux dérivées premières.
Exemple 1: y'' + w y=0 admet pour solutions sur R les fonctions j 1 (x) = sinw x et j 2 (x)= cos w x.
Exemple 2: Y''=0 admet pour solutions tout polynôme de la forme ax+b avec a et b deux constantes arbitraires.
On admettra que sous certaines conditions une équation différentielle du second ordre admet une infinité de solutions dépendantes de deux constantes arbitraires: y = j (x, l 1 ,l 2 ).
L'ensemble de ces solutions constitue l'intégrale
générale et représente l'équation d'une famille de courbes
dépendant de deux paramètres:
qui sont
appelées courbes intégrales. Une intégrale particulière est
obtenue en imposant des conditions initiales. Le plus souvent elles se présentent
de la forme y(x0)= yo et y'(x0)=y'0
. Dans ce cas, la courbe est assujettie à deux conditions: Passer par un point (x
0,y0) et avoir un coefficient de tangente donné y'0.
Remarque: En cinématique, les conditions initiales sont celles de la position du mobile et de sa vitesse à l'instant initial.
Inversement à toute courbe f(x, y, l 1, l 2 )=0 on peut associer une équation différentielle du second ordre.
Exemple: Soit la famille d'hyperboles
.
Les dérivées premières valent
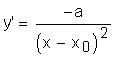et
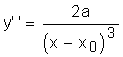. D'où l'équation différentielle qui régit cette famille de
courbes : y.y''=2.y'2 .
II EQUATIONS DIFFERENTIELLES SE RAMENANT AU PREMIER ORDRE
II-1 Equations ne contenant pas de y.
Soit F(x,y',y'')=0.
On pose y' = z(x), l'équation devient alors F(x, z, z' ) = 0.
Exemple: y'' + y'2 = 0.
On pose y' = z Þ
z' + z2 = 0 Þ
Þ
Þ
Þ
Þ
(x0 et y0 étant
des constantes).
II-2 Equations ne contenant pas de x.
F(y,y',y'')=0, et si on considère que y' est une fonction de y,
on peut donc poser 
et 
.
L'équation devient alors, avec pour nouvelle variable y,
qui est une
équation du premier ordre
pour z. Soit 
ou 
et en intégrant
avec
.
III EQUATIONS DIFFERENTIELLES LINEAIRES DU SECOND ORDRE
III-1 Définition.
On appelle équation différentielle linéaire du second ordre une équation de la forme
(1)
où a(x), b(x), c(x) et f(x) sont des fonctions.
On associe à cette équation l'équation sans second membre:
(ESSM)
III-2 Théorème fondamental.
La solution générale s'obtient en ajoutant à une intégrale particulière de l'équation complète (1) l'intégrale générale de l'équation sans second membre (ESSM).
.
III-3 Intégration de l'équation sans second membre.
(ESSM)
III-3-1 Si on connaît deux intégrales particulières y1 et y2 .
La solution générale s'écrit
.Les deux intégrales doivent être linéairement indépendantes,
ce qui se traduit par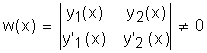 
( w(x) est appelé le Wronskien).
III-3-2 Si on connaît une intégrale particulière y1 .
On a donc: 
.
On pose 
où
z(x) est une fonction inconnue de x.
et
d'où en remplaçant dans (1)
a(x) (
) + b(x) (
)+ c(x)
= 0
Þ
.
Cette équation s'intègre comme une équation se ramenant à une équation du premier ordre (voir § II).
III-3-3 Si on ne connaît pas de solution particulière, ce n'est généralement pas intégrable sauf si a, b et c sont des constantes (voir § IV).
III-4 Intégration de l'équation complète.
III-4-1 Si on connaît une solution particulière yP .
La solution générale est alors
.
Exemple: L' équation (E)
admet pour solution de l'équation
sans second membre yESSM =
.A la
vue du second membre, l' intégrale particulière sera un polynôme
du troisième degré 
. On obtient
donc en remplaçant dans (E)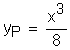 
.
D'où 
.
III-4-2 Si on ne connaît pas de solution particulière.
On applique la méthode de Lagrange appelée aussi méthode
de la variation de la constante. Elle ne doit être employée qu'en dernier
recours (surtout en physique). Soit l'intégrale générale de
l'équation sans second membre 
dans laquelle on va faire varier les constantes c'est à dire que
l
1 = l
1(x) et l
2 = l
2(x). L'équation différentielle fournissant une première
relation pour déterminer ces deux fonctions, il nous sera possible d'en imposer
une seconde.
On dérive 
pour obtenir 
.
On impose alors que 
(a).
En dérivant 
on obtient
et en reportant dans l'équation (1)
. Comme y1 et y2 sont des solutions particulières,
l' équation se simplifie en 
(b) où a(x) ¹
0, d'où le système
.
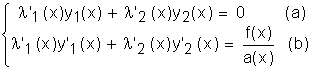Comme y1 et y2 sont linéairement
indépendantes .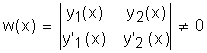
Le système précédent est un système de Cramer et détermine l '1 et l '2 , on a alors les solutions l 1(x) et l 2(x) qui par intégration dépendent chacune d'une constante arbitraire, d'où la solution générale.
Exemple: y'' + y = cotan x.
IV EQUATION LINEAIRE A COEFFICIENTS CONSTANTS
Soit l'équation 
où a, b et c sont des constantes.
La solution générale se présentera sous la forme
.
IV-1 Intégration de l'équation sans second membre
.
On cherche des solutions de la forme
, ce qui nous donne
et
et en remplaçant dans (ESSM) :
.
L'équation
est appelée équation caractéristique .
IV-1-1 D ¹ 0.
L'équation caractéristique admet deux racines distinctes
r1 et r2 . les fonctions
et 
sont deux intégrales
particulières de l'équation (ESSM) et
Dans le cas où D
<0 
(i²=-1), on pose
et
, 
devient
avec
En physique on posera
IV-1-2 D = 0.
On connaît une solution particulière de l'équation
sans second membre 
. On applique ensuite la
méthode générale, c'est à dire qu'on pose
, d'où
et
qu'on remplace dans
l' ESSM.
On obtient donc: 
. Comme 
= 0 et
= 0 car D
= 0 , z'' = 0 Þ
z' = l
1 Þ
z = l
1x + l
2 .
yESSM = ( l 1x + l 2).erx
IV-2 Solution particulière de l'équation
complète .
La méthode de Lagrange est en général
appliquée sauf dans les cas où le second membre se présente
sous la forme 
(polynôme de degré
n), 
, où encore
.
IV-2-1 
.
La solution particulière sera un polynôme
IV-2-2
.
Cherchons si 
est solution.
et
En remplaçant dans l'équation complète
on obtient après simplification par 
: 
, z(x) est donc un polynôme.
¹
0 alors m n'est pas racine de l'équation caractéristique, z(x) est
de degré n et 
= 0 et
¹
0 alors m est racine simple de l'équation caractéristique, z'(x)
est de degré n, z(x) est de degré n+1 et on démontre
facilement que 
= 0 et
= 0 alors m est racine double de
l'équation caractéristique, z''(x) est de degré n, z(x)
est de degré n+2 et on démontre que
IV-2-3 
.
On passe par les formules d'Euler afin de revenir
au cas précédent et le second membre devient f(x) = f1
(x) + f2 (x) avec 
.
Exemple: Trouver une solution particulière de
l' équation: 
.
Þ
On recherche d'une solution particulière de
. Le second membre est de la forme
, où n = 1 et m=2i.
L'équation caractéristique est 
or 
est racine simple d'où la forme
de l'intégrale particulière :
.
........etc...
