0. Introduction

1. Décomposition en somme d’intégrales
2. Changement de variables
3. Les produits trigonométriques
4. Les produits trigonométriques sous exposants
5. Intégration par parties

La formule 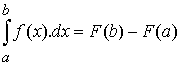ou montre la connaissance d’une primitive F(x). Les méthodes d’intégrations qui suivent ont pour but de se ramener à l’une des primitives ci-dessous que vous devez connaître :

1. Décomposition en somme d’intégrales

L’ensemble des fonctions intégrales sur [a ;b] forment un espace vectoriel Á _[a ;b] qui est sous-espace vectoriel des fonctions définies sur [a ;b].

D’où la première propriété :



Application aux polynômes :

Exemple 1 :

= =

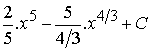
En présentant dans l’esprit du texte

Exemple 2 :

= = =

2. Changement de variables

 

3. Les produits trigonométriques

 

4. Les produits trigonométriques sous exposants

 

5. Intégration par parties