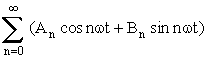
tutorés |
de réflexion |
SERIES DE FOURIER.
Développement en série de Fourier.
I DEFINITIONS.
1) Série de Fourier.
Soit f une fonction périodique, de période
![]() intégrable sur tout fermé de R, on appelle série de
Fourier de f, la série trigonométrique:
intégrable sur tout fermé de R, on appelle série de
Fourier de f, la série trigonométrique:
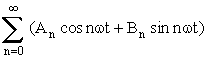
2) Théorème de Fourier.
Toute fonction périodique f, non sinusoïdale, continue sur tout intervalle
![]() =
=
![]() ( sauf éventuellement en un nombre fini de points de discontinuité
de première espèce ) et dérivable sur cet intervalle,
peut se décomposer en une somme infinie de fonctions sinusoïdales
dont les fréquences sont des multiples de celle de la fonction f:
( sauf éventuellement en un nombre fini de points de discontinuité
de première espèce ) et dérivable sur cet intervalle,
peut se décomposer en une somme infinie de fonctions sinusoïdales
dont les fréquences sont des multiples de celle de la fonction f:
f(t) = A0 + Y1 sin( w t – j 1) + Y2 sin(2w t – j 2) + ... + Y n sin(n w t – j n) + ... .
A0 = Terme constant, valeur moyenne (en mathématiques
on utilise aussi
![]() ).
).
Y1 sin(w t – j 1) = terme fondamental (harmonique de rang 1).
Y2 sin(2w t – j 2) = terme harmonique de rang 2.
Yn sin(nw t – j n) = terme harmonique de rang n.
ou encore
avec un(t) = Yn sin(n w t – j n ) = An cos(nw t) + Bn sin(nw t).
An = Yn cosj
n Yn = ![]()
Bn = Yn sinj
n j n =
 .
.
Remarque : La série de Fourier est convergente sur R.
3) Ecriture complexe.
un (t) = ![]() +
+
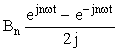
= ![]()
![]() +
+
![]()
![]()
en posant Cn =
![]()
= Cn![]() +
+
![]()
![]()
comme ![]() =
=
![]()
= Cn![]() +
+
![]()
![]()
d’où f(t) = A0 +
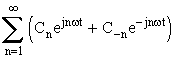
en posant C0 = A0 =
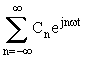
II CALCUL DES COEFFICIENTS.
On prendra ![]() et l’intervalle
et l’intervalle
![]() =
=
![]() .
.
1) Calcul de A0 .
![]() =
=
![]() +
+
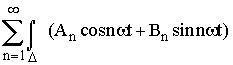 dt.
dt.
or 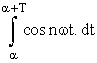 =
=
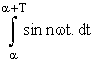 = 0
= 0
= A0.![]() = A0.T .
= A0.T .
2) Calcul de An.
Calculons 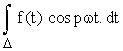
![]()
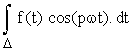 =
=
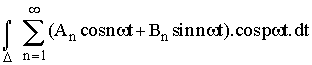
= 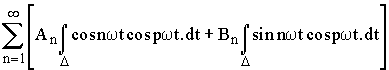
In Jn
In = 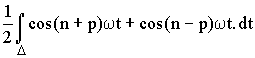 .
.
si ![]() In = 0
In = 0
si ![]() In =
In =
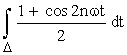
= 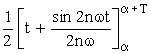
= ![]() .
.
Jn = 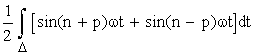 = 0
= 0
![]() n et p.
n et p.
D’où 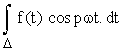 =
=
 = An.
= An.
![]() .
.
double de la valeur moyenne de f(t)cosn w t.
3) Calcul de Bn .
On calcule de même
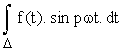 . p
Î N
. p
Î N
et
double de la valeur moyenne de f(t)sinn w t.
III PROPRIETES DES COEFFICIENTS
1) ![]()
2) Cas où f est une fonction paire
![]() =
=![]()
Bn = ![]() .
.
 = 0
" n
Î N*.
= 0
" n
Î N*.
An = ![]() .
.
 =
=
![]() .
.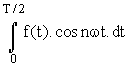 .
.
Dans le cas où f est paire, la série de Fourier est une série de cosinus avec
A0 = ![]() .
.
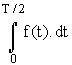 .
.
3) Cas où f est une fonction impaire
![]() =
=
![]() .
.
de même que précédemment
An = ![]() .
.
 = 0
"
n Î N.
Bn =
= 0
"
n Î N.
Bn = ![]() .
.
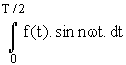
Si f est impaire, la série de Fourier est une série de sinus.
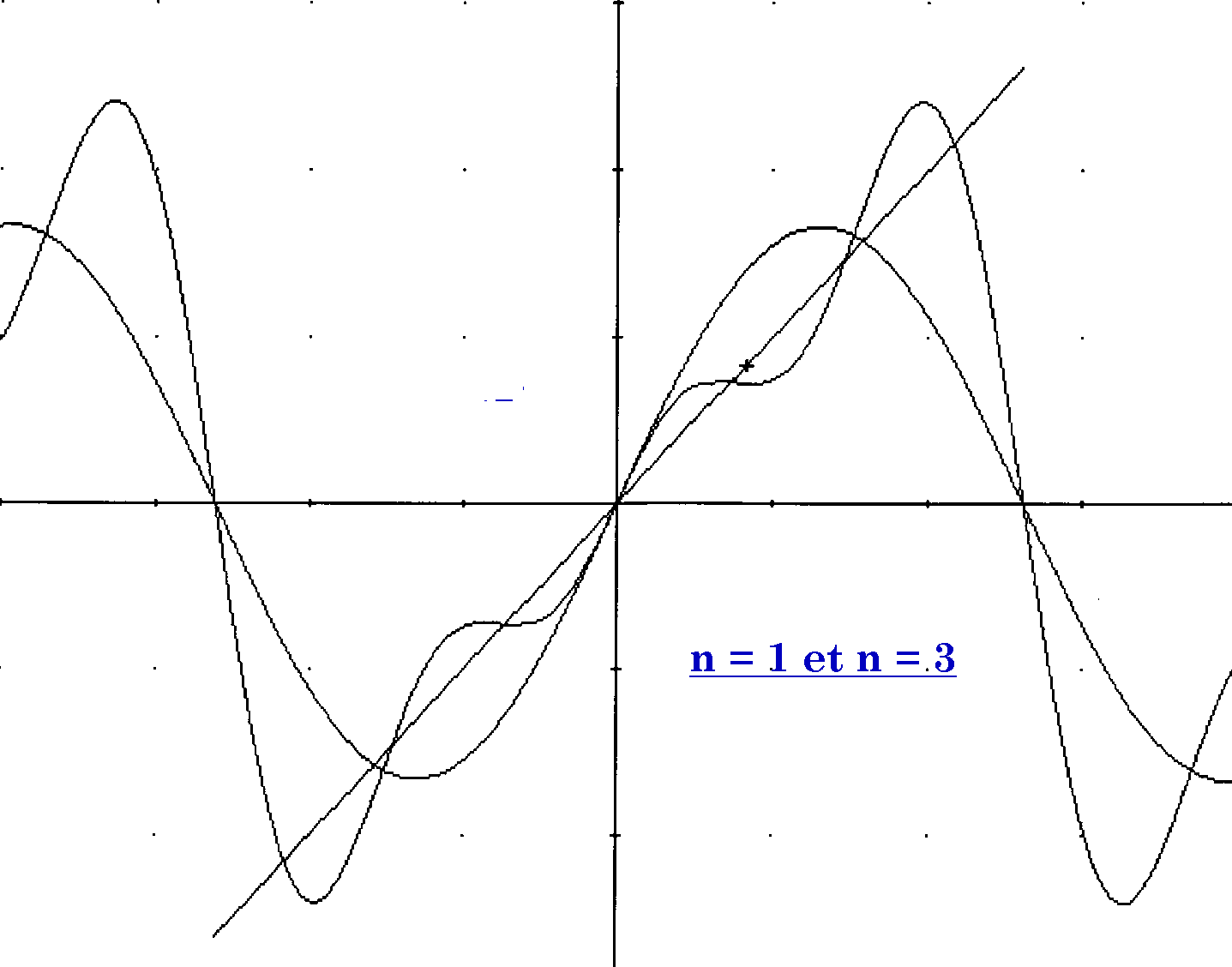
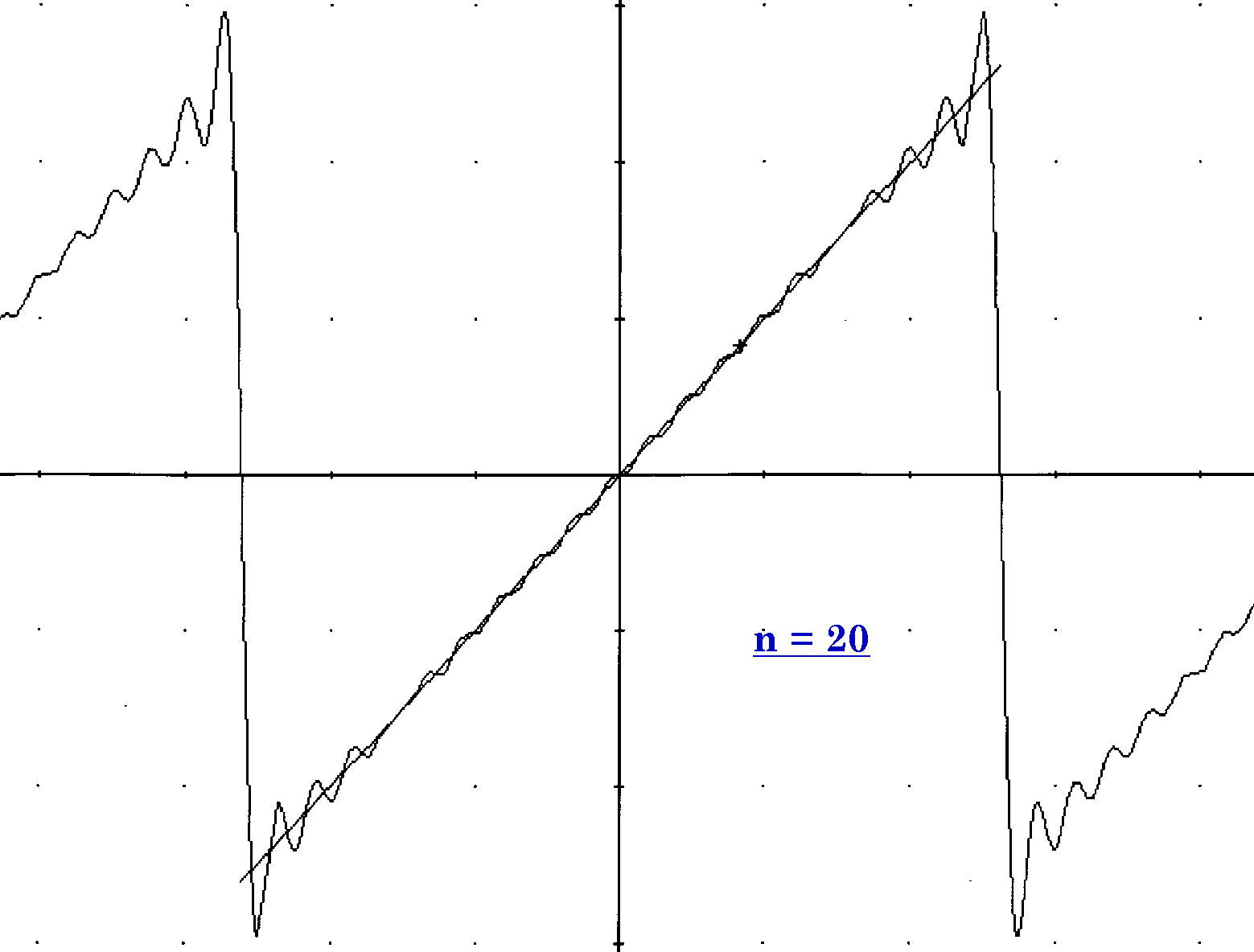
Exemple: Développez en série de Fourier la fonction f de période T = 2p définie par f(t) = t si t Î ] -p , p [.
Représentons cette fonction:
La fonction est impaire et se développe en une série de sinus.
An = 0
Calculons Bn
T = 2p w = 1
Bn = ![]() .
.
 =
=
![]() .
.
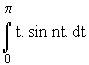
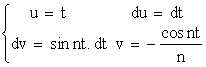
= ![]()
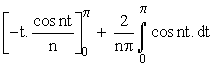
= ![]()
= ![]()
= ![]() =
=
![]() .
.
![]() .
.
d’où f(t) =
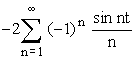
en développant f(t) = ![]()
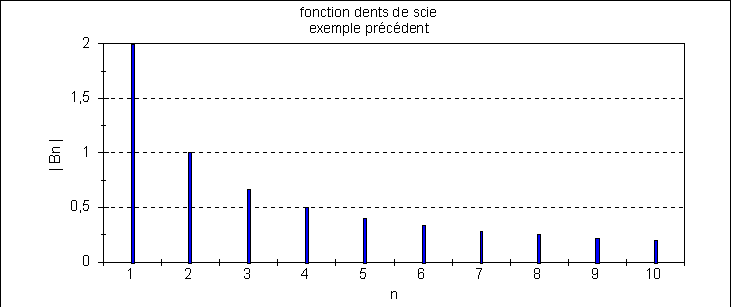
On remarque que la valeur des coefficients décroît (
![]() ).
).
4) Autres symétries.
![]() Þ A0 = 0 B2k = 0
Il n’y a pas de terme en sinus d’harmonique paire.
Þ A0 = 0 B2k = 0
Il n’y a pas de terme en sinus d’harmonique paire.
![]() Þ A2k = 0
Il n’y a pas de terme en cosinus d’harmonique paire.
Þ A2k = 0
Il n’y a pas de terme en cosinus d’harmonique paire.
et Þ B2k+1 = 0 Il n’y a pas de terme en sinus d’harmonique impaire.
![]() Þ B2k = 0 Il n’y a pas
de terme en sinus d’harmonique paire.
Þ B2k = 0 Il n’y a pas
de terme en sinus d’harmonique paire.
et Þ A2k+1 = 0 Il n’y a pas de terme en cosinus d’harmonique impaire.
5) Cas d’une fonction translatée.
Soit f une fonction périodique, développable en série de Fourier
f(t) =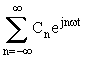 .
On considère la fonction g telle que g(t) = f(t – t0).
.
On considère la fonction g telle que g(t) = f(t – t0).
On montre que
Application: On appelle spectre de fréquence d’une fonction périodique du temps, le diagramme en bâtons obtenu en représentant |Cn | en fonction de n.
![]()
On représente aussi fréquemment en ordonnées le rapport
![]() , qui permet de relativiser
les harmoniques présentes par rapport au fondamental.
, qui permet de relativiser
les harmoniques présentes par rapport au fondamental.
Tout changement d’origine laisse le spectre invariant.
EExemple
: la fonction prise précédemment: f(t) =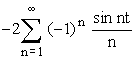 .( §III-3)
.( §III-3)