Soit un système ayant pour signal d'entrée e(t) et pour signal de sortie s(t).

Un système est dit linéaire s'il satisfait au principe de superposition:

- Si les réponses à deux signaux d'entrée e₁ et e₂ sont respectivement s₁ et s₂ ,
alors la réponse au signal a .e₁ + b .e₂ est a .s₁ + b .s₂ , pour tous coefficients a et b réels ou complexes.

Un système est invariant si un décalage dans le temps d'un signal d'entrée, entraîne le même décalage sur le signal de sortie:

- Si e(t) induit en sortie s(t) , alors e(t₁ + t₂ ) induit s(t₁ + t₂ ).

1) Soit e(t) un signal d'entrée périodique, de période T. Montrer que la sortie est périodique de même période.

2) On considère un signal d'entrée monochromatique, ,c'est à dire un signal du type e(t) = e^{2jp n t}.

2-a) Montrer que e(t) est périodique de période 1/n.

2-b) Montrer que e(t + u) = e(u).e^{2jp n t}.

2-c) En supposant t constant, montrer que: =.

2-d) s(0) représente la sortie au temps t=0 et dépend a priori de la fréquence n du signal d'entrée; s(0) est donc une fonction de n . On pose s(0) = H(n ).

Montrer que la sortie est égale à s(t) = H( n).e(t).

H(n ) est appelé fonction de transfert su système.

Considérons le circuit RC suivant:

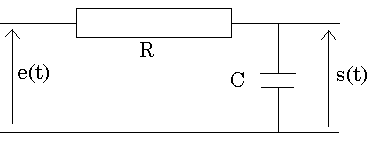
s(t) et e(t) sont liés par l'équation différentielle (1)

Après une période transitoire, d'un temps relativement court, la cellule RC entre en régime permanent et se comporte alors comme un système linéaire invariant.

1) Soit e(t) un signal monochromatique et d'après la première partie
on sait que s(t) = H(n).e(t).

1-a) En reportant cette équation dans l'équation (1), déterminer la fonction
de transfert H(n ).

1-b) Calculer le module de H(n ) et la limite du module quand n tend vers +µ .

2) On applique à l'entrée d'une cellule RC un signal sinusoïdal d'amplitude A, de fréquence n et de phase j : e(t) = A.cos(2p nt + j).

2-a) On note f (n) l'argument de H(n). En utilisant l'écriture exponentielle de H( n),
montrer que la sortie s'écrit: s(t) = A|H( n)|.cos(2.p. n.t + j + f(n)).

2-b) Quel est l'effet d'une cellule RC sur l'amplitude et la phase d'un signal sinusoïdal ?

2-c) On donne R= 100kW et C=300nF et le signal d'entrée . Calculer l'amplitude et la phase du signal de sortie dans les deux cas suivants:

n =10Hz ; n =50Hz.

3) On considère le signal e(t) triangulaire, pair et périodique de période T=1s
tel que e(t) = - 2t+1 pour tÎ [0,½].

3-a) Représenter e(t).

3-b) Calculer les coefficients de Fourier de e(t).

3-c) On applique e(t) à l'entrée d'une cellule RC. Montrer que la sortie s'écrit sous la forme .

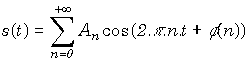3-d) En déduire la série de Fourier de s(t): .

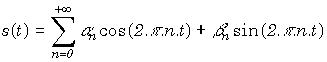On exprimera les coefficients a _n et b _n à l'aide de n, , et f (n).

Aller au cours

Retourner aux exercices tutorés

Retourner à la page d'accueil