Exercice I:

1) Pour l'argument, multiplier haut et bas par cosj , puis passer sous forme exponentielle

2) Du résultat précédent déduire l'écriture de z, puis identifier les parties réelle et imaginaire .

3) On applique la dernière relation à j = p /8 puis on pose y = tan(p /8).

4) En posant u=tan(x/2) et en utilisant les relations on obtient cosx en fonction de u. Pour calculer dx on partira comme suit:
d(tan(x/2) = du

On remarque que

1) Le module vaut 1 et l'argument 2j + 2kp

2) cos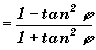2j , sin2j et tan2j

3) On obtient , la résolution donne deux solutions mais comme tan( p/8) est positive reste –1 + Ö2

4) l'intégrale
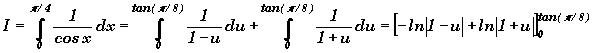