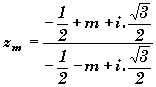Complexe ou compliqué
Exercice 1:
1) Calculer le module et l'argument du nombre complexe
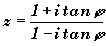 .
.
2) En déduire les expressions de sin2j
, cos2j
et tan2j
en fonction de tanj
.
3) Calculer tan(p
/8).
4) Utiliser ces résultats ainsi que le changement de variable
u=tan(x/2), pour calculer l'intégrale
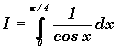
Exercice 2:
Sachant que 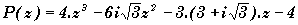 possède une racine réelle; résoudre dans
l'ensemble des complexes C
l'équation P(z) = 0.
possède une racine réelle; résoudre dans
l'ensemble des complexes C
l'équation P(z) = 0.
Exercice 3:
1) Déterminer l'ensemble des nombres complexes z qui vérifient:
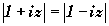
2) Soit a un nombre réel. Montrer que les solutions z de l'équation
(E): 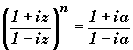 sont des nombres réels.
sont des nombres réels.
3) Résoudre l'équation (E).
Exercice 4:
m étant un paramètre réel, on
considère le nombre complexe
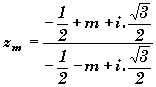
1) Calculer la partie réelle et la partie imaginaire de
zm .
2) Déterminer les valeurs de m pour lesquelles la partie réelle de
zm est nulle. Calculer le module et l'argument de
zm pour chacune des valeurs de m obtenues.
3) Résoudre dans C
l'équation 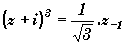 .
.
( z–1 désigne zm pour
m = –1)
Exercice 5:
Soit z = x + i.y un nombre complexe quelconque. On appelle
ez le nombre complexe de module ex
et d'argument y.
On peut donc écrire:
ez = ex + i.y = ex . ei.y .
1) Montrer que pour tout z et z' dans
"
, ez + z' = ez .ez' .
2) Montrer que 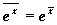 .
.
3) Démontrer que 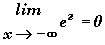
4) Démontrer: "
z Î
C
|ez|£
e|z| .
5) Résoudre les équations:
ez = –1 ; ez = –3 ;
ez = i .
Aller au cours sur les complexes

Accueil
Cours
Exercices tutorés
Exercices de rélexion
Formulaires

![]() .
.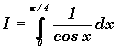
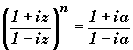 sont des nombres réels.
sont des nombres réels.