Exercice III:
Aide:
1) Factoriser respectivement par i et –i dans chacun
des membres, puis suivre un raisonnement géométrique en prenant
trois points M, A, et B d'affixes respectives
z
, i, et –i.
2) Les modules d'un complexe et de son conjugué sont égaux
et
|zn|= |z|n
3) Calculer le module et l'argument des deux membres puis égaler les écritures exponentielles.
Corrigé:
1) Comme 
alors MA = MB
, donc les points M constitue la médiatrice de [A,B].
Or cette droite est l'axe des réels , cela signifie que z est réel
2) Si a est un réel 1+ia et 1–ia sont
conjugués, ils ont le même module et le complexe
est de module
1.
L'équation (E) implique l'égalité des modules:
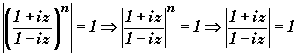
Ce qui entraîne que z est réel.
3) Résolution de l'équation (E).
Si a est un réel, le complexe
est de module
1; il s'écrit alors ei.q
avec:
D'où l'écriture:
et de même
(car z est réel)
On obtient 
L'équation (E) possède ainsi n solutions:
