La femme est le chef d'oeuvre de Dieu surtout quand elle a le diable au corps {Alphonse Allais}

Logarithmes

I) Etudier les fonctions:
y = x.lnx y = ln|lnx| y = x.lnx – x y = ln|x² – 4x + 1|

II) Calculez les dérivées de
y = ln|sinx|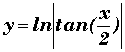

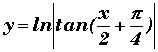III) Utiliser les dérivées logarithmiques pour déterminer les dérivées suivantes:
y = (x² + 2)³.(1– x³)⁴ y = x^x y = x^lnx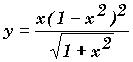

IV) Trouver les primitives de

V) Résoudre
ln(3x) = 1 + lnx ln(x² – 1) = ln(2x – 1) – ln2

VI) Résoudre les systèmes

VII) Résoudre les systèmes

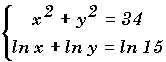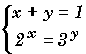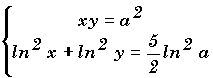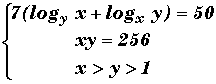VIII) Etablir log_a b . log_b c . log_c d ... log_z a = 1

IX) Quelle relation exis-t-il entre a, b et c si l'on a:

X) Etudiez les fonctions

y = x + ln(x² – 1)

XI) Montrer que
pour 0 < x < 1 on a ln(1+x) < x < – ln(1–x)

En déduire 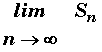avec et n et k entiers naturels.